If you’ve worked with Verilog or SystemVerilog, you’ve likely encountered the term race condition—and, if you’re like most engineers, you may not fully understand why they happen or how to avoid them. If that’s the case, don’t worry; you’re certainly not alone. Even seasoned experts with decades of experience, myself included, occasionally run into race conditions.
Despite being a well-known problem, there is surprisingly little educational material on Verilog race conditions. In fact, when I set out to write this article, I asked several large-language models for common examples of race conditions. Interestingly, none of them provided valid examples, and many were outright misleading. This suggests that the lack of quality training data on race conditions—specifically, well-documented, accurate examples—has led to poor results even from advanced AI systems.
In this article, I’ll provide a clear explanation of the concepts behind race conditions, how they arise in Verilog and SystemVerilog, and practical strategies for avoiding them. By the end, you’ll have a solid foundation for identifying and preventing race conditions in your own designs.
What is a race condition?
In general computing, a race condition (sometimes simply referred to as a “race”) occurs when the behavior of a program changes depending on the order in which different regions of code are executed. Typically, race conditions arise in concurrent or parallel systems, where multiple processes are running at the same time. In such systems, the final outcome can depend on the timing of each process’s execution. As a result, most programmers working with sequential code are unlikely to encounter race conditions.
Verilog, however, is particularly susceptible to race conditions because of its many parallel constructs. During a Verilog simulation, most simulators don’t execute all processes simultaneously; rather, they process each one sequentially—one process at a time, cycling through them repeatedly.
In Verilog and other parallel languages, the order in which processes are executed is deliberately not specified by the language. The reason for this design choice is straightforward: imagine the programmer having to determine the execution order of potentially thousands of processes. This would be an impractical—and virtually impossible—task. As a result, simulators are free to execute processes in any order they choose.
This arbitrary execution order is what leads to race conditions. Ideally, we want to write Verilog code whose behavior remains consistent, regardless of the simulation order. However, achieving this consistency can be surprisingly difficult without a solid understanding of how race conditions occur and how to avoid them.
Simple Example
The following example illustrates a common race condition:
`timescale 1ns / 100 ps
module race1 #(
parameter int NUM_TESTS = 100,
parameter int WIDTH = 8
);
logic clk = 1'b0;
logic [WIDTH-1:0] count1 = '0;
logic [WIDTH-1:0] count2 = '0;
initial begin : generate_clock
forever #5 clk = ~clk;
end
initial begin : counter1
for (int i = 0; i < NUM_TESTS; i++) begin
count1++;
@(posedge clk);
end
$display("Tests completed.");
disable generate_clock;
end
always @(posedge clk) begin : counter2
count2++;
assert (count1 == count2);
end
endmoduleThis example consists of three processes, using a mix of initial and always blocks. The first process generates a clock signal to synchronize the other processes. The second process, counter1, contains a loop that increments the count1 signal, then waits for the rising edge of the clock before repeating. The third process, counter2, behaves similarly but waits for the rising clock edge, increments its local count2 signal, and then compares count1 and count2.
The intent of this code is to verify that count1 and count2 remain equal. What makes race conditions particularly tricky is that this code may appear to work in many simulators. For example, when running it in Questa Sim-64 2023.2_1, the simulation completes without any assertion failures:

However, as we will see, the correctness of the code is entirely dependent on the order in which the processes are simulated.
Let’s rewrite the code in a way that should be semantically equivalent:
`timescale 1ns / 100 ps
module race2 #(
parameter int NUM_TESTS = 100,
parameter int WIDTH = 8
);
logic clk = 1'b0;
logic [WIDTH-1:0] count1 = '0;
logic [WIDTH-1:0] count2 = '0;
initial begin : generate_clock
forever #5 clk = ~clk;
end
initial begin : counter1
for (int i = 0; i < NUM_TESTS; i++) begin
count1++;
@(posedge clk);
end
$display("Tests completed.");
disable generate_clock;
end
initial begin : counter2
forever begin
@(posedge clk);
count2++;
assert (count1 == count2);
end
end
endmoduleIn this modified version, the always_ff block from process counter2 has been replaced with an initial block that loops indefinitely, first waiting for a clock edge. These changes preserve the exact semantics of the previous always_ff block, so any differences in simulation behavior must stem from other issues in the code. Let’s see if that’s the case:
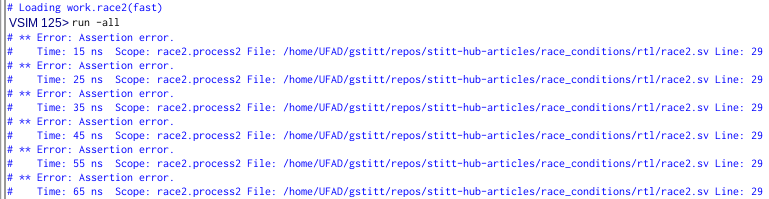
We have confirmed a race condition! Two examples that should yield identical results are producing different outputs. Many people might initially assume that the always_ff block is the “correct” solution and that the initial block version is “incorrect.” However, this assumption is flawed. In fact, one of the most dangerous assumptions you can make is that just because you are getting the right output, there must not be any race conditions.
It turns out that both examples are incorrect. The first one simply got lucky— the simulator chose a simulation order that happened to produce the intended output, while the second version did not. Let’s step through the simulation and see if we can identify the underlying problem.
Initially, the simulator executes the counter1 and counter2 processes until they reach the clock synchronization statements. After the first clock edge, the simulator resumes execution of both processes. However, since the simulator must sequentially execute these processes, there are two possible outcomes. First, let’s consider the scenario where the simulator resumes execution of the counter2 process first:
count1++; // counter1 (count1 == 1)
@(posedge clk);
count2++; // counter2 (count2 == 1)
assert(count1 == count2); // assertion passes
count1++; // counter1 (count1 == 2)
@(posedge clk);
count2++; // counter2 (count2 == 2)
assert(count1 == count2); // assertion passes
count1++; // counter1 (count1 == 3)
etc.
In this scenario, the simulation behaves as the designer likely intended. The counter2 process updates count2, and the comparison succeeds because it matches count1 from the counter1 process. However, there is no guarantee that, after the clock edge, the simulator will resume simulating the counter2 process before counter1. Let’s now examine what happens when the simulator resumes the counter1 process first:
count1++; // counter1 (count1 == 1)
@(posedge clk);
count1++; // counter1 (count1 == 2)
count2++; // counter2 (count2 == 1)
assert(count1 == count2); // assertion fails
@(posedge clk);
count1++; // counter1 (count1 == 3)
count2++; // counter2 (count2 == 2)
assert(count1 == count2); // assertion fails
etc.
In this case, the counter1 process increments count1 a second time before the counter2 process executes. The simulator then resumes the counter2 process, which updates count2. However, since count2 has only been incremented once while count1 has been incremented twice, the assertion fails.
The fact that two different simulation orders produce different results proves that this code suffers from a race condition. However, let’s confirm that the simulation order is the cause. To do this, we’ll use the following modified race2 module, which prints out the counts:
`timescale 1ns / 100 ps
module race2_debug #(
parameter int NUM_TESTS = 100,
parameter int WIDTH = 8
);
logic clk = 1'b0;
logic [WIDTH-1:0] count1 = '0;
logic [WIDTH-1:0] count2 = '0;
initial begin : generate_clock
forever #5 clk = ~clk;
end
initial begin : counter1
$timeformat(-9, 0, " ns");
for (int i = 0; i < NUM_TESTS; i++) begin
count1++;
$display("[%0t] count1 = %0d", $realtime, count1);
@(posedge clk);
end
$display("Tests completed.");
disable generate_clock;
end
initial begin : counter2
forever begin
@(posedge clk);
count2++;
$display("[%0t] count2 = %0d", $realtime, count2);
assert (count1 == count2);
end
end
endmoduleHere is the output from this code:

The actual simulation order closely follows our manual simulation, with one slight difference. Initially, at time 0, the counter1 process increments count1 as expected, then waits for a clock edge. After the clock edge, the simulator resumes execution of the counter2 process first, incrementing count2, which causes the assertion to pass. The simulator then resumes the counter1 process and increments count1 again.
So far, the simulation order matches our manual recreation, which worked as expected. However, something unusual happens in the next time step. After the clock edge, counter1 resumes first and increments count1. Then counter2 resumes and increments count2. At this point, count1 has been incremented twice in a row, causing the assertion to fail—just like in our second recreation. This issue repeats in every subsequent iteration, with counter1 always resuming before counter2.
You might have a few questions. For example, why did the simulator initially resume counter2 before counter1 after the first clock edge, only to change the order later? And why did the original always_ff block always resume counter2 before counter1?
Surprisingly, there are no definitive answers to these questions without knowing how a particular simulator is implemented. Ultimately, because SystemVerilog does not impose an ordering on process simulation, the simulator can execute processes in any order it chooses. I’ve encountered situations where the simulation order shifts during execution—similar to the difference we see between the first and subsequent iterations in the example above. There’s no point in adjusting the code to account for a specific order, as a different simulator might handle things differently. Even the same simulator might change its simulation order when the code changes.
Ultimately, we need a solution that works for any ordering of processes. Before we take a look at that solution, let’s first examine a more complete example that represents a common scenario where designers accidentally introduce race conditions.
Accumulation Testbench
While the previous example was synthetic, the type of race condition it demonstrated is actually quite common in many testbenches. To see how this race manifests in a more realistic scenario, let’s examine some testbenches for the following accumulator:
module accum #(
parameter int IN_WIDTH = 16,
parameter int OUT_WIDTH = 32
) (
input logic clk,
input logic rst,
input logic en,
input logic [ IN_WIDTH-1:0] data_in,
output logic [OUT_WIDTH-1:0] data_out
);
always_ff @(posedge clk) begin
if (en) data_out <= data_out + data_in;
if (rst) data_out <= '0;
end
endmoduleThis code implements a simple accumulator that adds data_in to the current data_out whenever the enable en signal is asserted.
Now, let’s take a look at a common testbench style:
`timescale 1ns / 100 ps
module accum_tb_race1 #(
parameter int NUM_TESTS = 10000,
parameter int IN_WIDTH = 8,
parameter int OUT_WIDTH = 16
);
logic clk = 1'b0;
logic rst;
logic en;
logic [IN_WIDTH-1:0] data_in = '0;
logic [OUT_WIDTH-1:0] data_out;
accum #(
.IN_WIDTH (IN_WIDTH),
.OUT_WIDTH(OUT_WIDTH)
) DUT (
.clk (clk),
.rst (rst),
.en (en),
.data_in (data_in),
.data_out(data_out)
);
initial begin : generate_clock
forever #5 clk = ~clk;
end
initial begin : data_in_driver
rst = 1'b1;
@(posedge clk);
rst = 1'b0;
@(posedge clk);
forever begin
data_in = $urandom;
@(posedge clk);
end
end
initial begin : en_driver
en = 1'b1;
forever begin
@(posedge clk iff !rst);
en = $urandom;
end
end
int test = 0;
logic [OUT_WIDTH-1:0] model = '0;
initial begin : monitor
@(posedge clk iff !rst);
while (test < NUM_TESTS) begin
if (en) begin
model += data_in;
test++;
end
assert (data_out == model);
@(posedge clk);
end
$display("Tests completed.");
disable generate_clock;
end
endmoduleThis testbench contains several processes. The first generates the clock. The second, data_in_driver, drives the rst and data_in signals. The third process, en_driver, randomly toggles the enable signal after the reset is cleared. The fourth process, monitor, acts as a monitor and evaluator: it detects outputs, updates the reference model, and verifies the output.
Before moving on, take a moment to see if you can spot any race conditions. There are several.
When creating this testbench, the designer likely assumed a specific simulation order for each test: after each clock edge, the simulator would first execute monitor, followed by data_in_driver, and then en_driver. The expected simulation order would look like this:
@(posedge clk);
model += data_in; // monitor
assert (data_out == model);
data_in = $urandom; // data_in_driver
en = $urandom; // en_driver
@(posedge clk);
etc.
If the simulator happens to choose this simulation order, the code appears to function correctly, despite the presence of race conditions. However, this was not the simulation order I encountered. I immediately observed an issue at the start of the simulation:
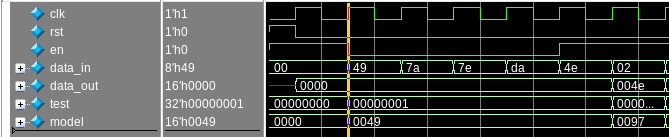
At the position of the cursor, you can immediately spot a discrepancy between the model and data_out. In fact, data_out is correct here, but the model itself is wrong. While it may seem that the modeling code is at fault, this is highly unlikely, especially since it only required a single line of code. The issue isn’t with the model, but rather with a race condition that’s corrupting its behavior. The following diagram illustrates the actual simulation order (reset is ignored for now):
data_in = 8'h00;
en = 1'b1;
model = '0;
@(posedge clk);
data_in = 8'h49; // data_in_driver (data_in = 8'h49)
model += data_in; // monitor (model = 16'h49)
assert (data_out == model); // assertion fails (0 != 16'h49)
en = 1'b0; // en_driver
@(posedge clk);
etc.
Essentially, the simulator is executing the data_in_driver process before the monitor, causing data_in to be updated earlier than intended, which results in a corrupted model. Meanwhile, data_out is correct because it is based on the previous value of data_in, but because it differs from the corrupted model, the assertion fails.
Similarly, another race condition that could occur is the following:
@(posedge clk);
en = 1'b0; // en_driver clears enable before monitor has been updated
if (en) ... // monitor doesn't update model because en cleared early
assert (data_out == model); // assertion fails because model not updated
data_in = 8'h49; // data_in_driver
@(posedge clk);
etc.
In this situation, after each clock edge, the simulator first executes en_driver, then monitor, and finally data_in_driver. This code fails because the designer assumed the monitor would execute before the enable driver. When it doesn’t, the enable signal is modified for the next test, either preventing the model from being updated (as shown) or updating the model unnecessarily.
There’s another race condition that is completely unrelated to the simulation order of the testbench processes. Consider the reset. After asserting the reset signal, both the testbench and the accum instance are synchronized by the clock signal. On the next clock edge after the reset is asserted, the simulator will simulate: 1) rst = 1'b0 in data_in_driver, and 2) the always_ff block in the accum module. How do we know which task is simulated first? We don’t. Let’s consider both possibilities:
// data_in_driver
rst = 1'b0;
// accum always_ff
if (en) data_out <= data_out + data_in;
if (rst) data_out <= '0; // data_out not reset
If the simulator first clears the reset, the accum instance will see rst == 0 and will not reset the data_out signal. The simulator could also do this instead:
// accum always_ff
if (en) data_out <= data_out + data_in;
if (rst) data_out <= '0; // reset occurs
// data_in_driver
rst = 1'b0;
If the simulator simulates the accum instance first, the always_ff block will see rst == 1'b1 and reset data_out. These differences are very dangerous. We now have a race condition where a module might come out of reset at different times in different simulations. Even worse, consider a more complex design where our DUT has thousands of always_ff blocks that rely on this reset. Since the simulator can process these blocks in any order, different always_ff blocks could be in different reset states during the same simulation. This can lead to catastrophic results.
How Not to Fix a Race Condition
When encountering a race condition like the ones described above, the first instinct is often to make various tweaks in an attempt to “fix” it. This is a dangerous approach, as some of these tweaks might make the issue seem to be resolved, while in reality, the race condition remains.
A common bad habit I frequently see is adding small wait statements within the problematic task. For instance, in the accumulator testbench above, the simulator updated data_in before the monitor could read the previous value. A natural response to this issue is to try to force the simulator to execute the monitor first by manually inserting a wait statement. For example:
initial begin : data_in_driver
rst = 1'b1;
@(posedge clk);
rst = 1'b0;
@(posedge clk);
forever begin
#1;
data_in = $urandom;
@(posedge clk);
end
endThis coding change technically addresses one race condition, as it ensures that if the simulator resumes data_in_driver before the monitor, the task will immediately wait, forcing the simulator to switch to the other tasks. This allows the monitor to execute without data_in being updated too early.
However, this approach is non-ideal for several reasons. First, the waveform becomes awkward, as now all the inputs are delayed relative to the clock edge:

If you’re using this approach to model a circuit delay, it can be an acceptable practice. However, I strongly discourage it as a way to resolve race conditions.
A second, and usually more significant, reason to avoid this practice is that race conditions will often remain unresolved, requiring additional waits in other places. Each time you add a wait, the code and waveform become more difficult to follow. For large testbenches with numerous tasks, managing all the waits eventually becomes overwhelming.
In summary, if you find yourself adding seemingly extraneous wait statements to resolve testbench issues, it’s likely a sign that the problem should be addressed in a different way. In my experience, I’ve never encountered a situation where waits were necessary to resolve race conditions.
So, how do we solve race conditions more generally?
Non-Blocking Assignments Are Your Best Friend
While race conditions can have many causes, in my experience, the examples above illustrate the most common one. At the core of the issue is the fact that we have multiple tasks sharing a variable, all synchronized to the same event (e.g., a clock edge). Since manually forcing a simulation order isn’t practical, what can we do to solve this problem?
Ultimately, we need to make our code independent of the simulation order. However, this isn’t feasible with blocking assignments. Fortunately, we can easily resolve all the examples above by using non-blocking assignments.
Non-blocking assignments are useful here because all signals assigned with a non-blocking assignment update their values simultaneously at the end of the current time step. This is exactly what we need, as the issue we encountered earlier was caused by signals changing unexpectedly. By ensuring that all signal values update at the end of the time step, we can guarantee deterministic behavior, regardless of the simulation order.
I’ve noticed that many people use non-blocking assignments simply because they were taught to do so at some point. To fully understand how they address race conditions, however, we need a clearer understanding of their behavior. While the low-level simulation mechanics of non-blocking assignments are quite complex, you don’t need to dive into that much detail unless you’re designing a simulator yourself.
I like to think of non-blocking assignments as having both a current value and a future value. In contrast, blocking assignments only have a current value. Let’s look at a simple example to illustrate this concept:
module nonblocking_test;
logic clk = 1'b0;
int x;
initial begin
forever #5 clk <= ~clk;
end
initial begin
$timeformat(-9, 0, " ns");
x <= 0; // Current = 'X, Future = 0
@(posedge clk) // Current = Future
x <= 1; // Current = 0, Future = 1
$display("%0d", x); // Prints 0
x <= 2; // Current = 0, Future = 2
$display("%0d", x); // Prints 0
@(posedge clk); // Current = Future
$display("%0d", x); // Prints 2
end
endmoduleWhen using a non-blocking assignment, the current value of a variable isn’t changed immediately. Instead, its future value is set to be assigned at the end of the current time step. On line 11, the assignment sets x‘s future value to 0, while the current value remains unchanged. In fact, the current value is undefined since this is the first time step. When the clock edge occurs on line 12, it ends the time step, and x‘s future value (0) is assigned to its current value. Next, line 13 doesn’t modify x‘s current value of 0; it only sets the future value to 1, so line 14 prints 0. Similarly, line 15 doesn’t change the current value of x; it only updates the future value from 1 to 2. On line 17, waiting for the clock edge ends the time step and causes the simulator to update the current value (0) with the future value (2). Since x has now been updated, line 18 prints the current value of 2.
There are two other ways I like to think of non-blocking assignments. First, when you read from a variable assigned via a non-blocking assignment, you’re always accessing the value from the previous time step. No matter how many times it is assigned, the value doesn’t actually change until the end of the current time step. Alternatively, I think of a non-blocking assignment as being similar to a hardware register. The assignment is analogous to changing a register’s input, where the register’s output doesn’t update immediately, but on the next rising clock edge. The key difference is that for a non-blocking assignment, the update happens at the end of the current simulation time step. It’s not a coincidence that we typically use non-blocking assignments to describe registers, because for a register, the next time step is the next rising clock edge, making the two behaviors equivalent.
Since it is generally considered bad practice to use wait statements in synthesizable code, outside of testbenches, you can usually think of the end of a time step as being equivalent to the end of an always block. Testbenches, however, are more complex, so you need to account for all explicit waits (e.g., #1, @(posedge clk), etc.) in addition to the end of always blocks.
To further reinforce that the order of non-blocking assignments doesn’t matter within a single time step, consider the following example:
`timescale 1ns / 100 ps
module nonblocking_test2;
logic clk = 1'b0;
initial begin : generate_clock
forever #5 clk <= ~clk;
end
int a1 = 0, a2 = 0, a3 = 0;
int b1 = 0, b2 = 0, b3 = 0;
int c1 = 0, c2 = 0, c3 = 0;
initial begin
for (int i = 0; i < 100; i++) begin
for (int j = 0; j < 100; j++) begin
a1 <= i;
b1 <= j;
c1 <= a1 + b1;
a2 <= i;
c2 <= a2 + b2;
b2 <= j;
c3 <= a3 + b3;
a3 <= i;
b3 <= j;
@(posedge clk);
end
end
$display("Tests completed.");
disable generate_clock;
end
assert property (@(posedge clk) c1 == c2);
assert property (@(posedge clk) c2 == c3);
assert property (@(posedge clk) c1 == c3);
endmoduleThis example explicitly tests the semantics of different orders by varying the sequence of assignment statements. In the first test, c1 is assigned after a1 and b2. In the second test, c2 is assigned between a2 and b2. Finally, in the third test, c3 is assigned before a3 and b3.
If you’re not comfortable with non-blocking assignments, it might be surprising that c1, c2, and c3 are always identical, as confirmed by the assertion statements during simulation. The result for c3 is especially surprising, considering it’s assigned before its corresponding inputs, a3 and b3, are assigned.
The key point to remember is that none of these assignments change the value of their corresponding variable until the @(posedge clk) statement. This means that all the values on the right-hand side of the assignments are from the previous time step. As a result, the order of assignments doesn’t affect the behavior. Similarly, different simulation orders of non-blocking assignments also do not change the behavior. In other words, non-blocking assignments offer a general solution to many race conditions.
Solving the Original Race Conditions
Let’s now apply non-blocking assignments to fix the original problematic examples. There is one crucial rule to keep in mind: any signal assigned in one process and read in another—where both the assignment and the read are synchronized to the same event—should be assigned using a non-blocking assignment. This rule can be a little confusing at first, so let’s see some examples of how to apply it.
The violation of the rule in the original race1 and race2 examples came from count1 being assigned (with a blocking assignment) in one process (on line 17) and read in another process (on lines 27/29), both of which are synchronized to the same @(posedge clk) event.
If we apply this rule to the original race1 and race2 examples, all we need to do is change the assignment of count1 to a non-blocking assignment, and we get the following corrected code, which resolves the race conditions:
`timescale 1ns / 100 ps
module no_race #(
parameter int NUM_TESTS = 100,
parameter int WIDTH = 8
);
logic clk = 1'b0;
logic [WIDTH-1:0] count1 = '0;
logic [WIDTH-1:0] count2 = '0;
initial begin : generate_clock
forever #5 clk = ~clk;
end
initial begin : counter1
for (int i = 0; i < NUM_TESTS; i++) begin
count1 <= count1 + 1'b1;
@(posedge clk);
end
$display("Tests completed.");
disable generate_clock;
end
initial begin : counter2
forever begin
@(posedge clk);
count2++;
assert (count1 == count2);
end
end
endmoduleLet’s now analyze why this resolves the race condition, using the simulation order that previously exposed the problem, where the counter1 process resumed before counter2:
count1 <= count1 + 1; // counter1 (current count1 = 0, future count1 = 1)
@(posedge clk); // count1 becomes 1 at end of time step
count1 <= count1 + 1; // counter1 (current count1 = 1, future count1 = 2)
count2++; // counter2 (count2 == 1)
assert(count1 == count2); // assertion passes because current count1 == 1
@(posedge clk); // count1 becomes 2 at end of time step
count1 <= count1 + 1; // counter1 (current count1 = 2, future count1 = 3)
count2++; // counter2 (count2 == 2)
assert(count1 == count2); // assertion passes because current count1 == 2
etc.
Let’s double-check that the other simulation order doesn’t introduce any issues:
count1 <= count1 + 1; // counter1 (current count1 = 0, future count1 = 1)
@(posedge clk); // count1 becomes 1 at end of time step
count2++; // counter2 (count2 == 1)
assert(count1 == count2); // assertion passes
count1 <= count1 + 1; // counter1 (current count1 = 1, future count1 = 2)
@(posedge clk); // count1 becomes 2 at end of time step
count2++; // counter2 (count2 == 2)
assert(count1 == count2); // assertion passes
count1 <= count1 + 1; // counter1 (current count1 = 2, future count1 = 3)
etc.
Both simulation orders work! You might be wondering why I only changed one assignment to non-blocking. I could have also changed count2 on line 28, but doing so would have required modifying the timing of the assertion, or else the assertion would not have used the updated count2 value. Remember the rule: any signal that is assigned in one process and read in another, where both the assignment and read are synchronized to the same event, should be assigned using a non-blocking assignment. In this example, the only signal to which this rule applies is count1.
You might also be wondering about the clock signal and whether it requires a non-blocking assignment as well. After all, it’s assigned in one process and read in multiple processes. To avoid overwhelming the reader with low-level intricacies of the race-condition rule, it’s sufficient to say that using a non-blocking assignment for the clock would be safer. For reasons discussed below, this particular case doesn’t cause a race condition, but in general, it could. So, it’s better to always use a non-blocking assignment for the clock.
Now that we’ve solved the simple example, we can easily apply the same approach to solve the race conditions in the accum testbench. Here is a corrected version of the testbench:
`timescale 1ns / 100 ps
module accum_tb #(
parameter int NUM_TESTS = 10000,
parameter int IN_WIDTH = 8,
parameter int OUT_WIDTH = 16
);
logic clk = 1'b0;
logic rst;
logic en;
logic [IN_WIDTH-1:0] data_in = '0;
logic [OUT_WIDTH-1:0] data_out;
accum #(
.IN_WIDTH (IN_WIDTH),
.OUT_WIDTH(OUT_WIDTH)
) DUT (
.clk (clk),
.rst (rst),
.en (en),
.data_in (data_in),
.data_out(data_out)
);
initial begin : generate_clock
forever #5 clk <= ~clk;
end
initial begin : data_in_driver
rst <= 1'b1;
@(posedge clk);
rst <= 1'b0;
@(posedge clk);
forever begin
data_in <= $urandom;
@(posedge clk);
end
end
initial begin : en_driver
en <= 1'b1;
forever begin
@(posedge clk iff !rst);
en <= $urandom;
end
end
int test = 0;
logic [OUT_WIDTH-1:0] model = '0;
initial begin : monitor
@(posedge clk iff !rst);
while (test < NUM_TESTS) begin
if (en) begin
model <= model + data_in;
test++;
end
assert (data_out == model);
@(posedge clk);
end
$display("Tests completed.");
disable generate_clock;
end
endmoduleWhen working with a testbench, there’s an easier-to-remember specialization of the rule for non-blocking assignments: every DUT input should be driven by a non-blocking assignment. Why is this the case? It’s really just an application of the general rule. DUT inputs are typically driven in one process and read in others, while being synchronized by a clock signal. As a result, a blocking assignment to any DUT input can potentially cause a race condition. Notice that en, data_in, rst, and clk all use non-blocking assignments in my corrected code.
While there are situations where using a blocking assignment on a particular input won’t cause a race condition, it’s not worth the effort to determine which inputs can safely use blocking assignments. It’s much safer to simply assign all DUT inputs with non-blocking assignments. For example, in this code, we could have used a blocking assignment for the clock signal without causing a race condition because the clock is only used for synchronization and never appears on the right-hand side of a statement. However, if the DUT or testbench performed any logic with the clock (e.g., clock gating), a blocking assignment could have caused race conditions. Since there is no benefit to using a blocking assignment for the clock, the best practice is to always use a non-blocking assignment.
Notice that on line 56, I also made model use a non-blocking assignment. I did this because, without it, the comparison between model and data_out would have used the new version of model but the previous version of data_out, which would have caused assertion failures. Alternatively, I could have left the model assignment as blocking and moved the assertion to after the clock edge to ensure data_out is updated. In many cases, you’ll need to carefully consider the timing of your model and DUT outputs, since they might differ if one uses blocking and the other uses non-blocking assignments.
Finally, let’s analyze one of the simulation orders that previously exposed a race condition:
data_in <= 8'h49; // data_in_driver (Current = 0, future = 8'h49)
model <= model + data_in; // monitor (current = 0, future = 16'h49)
assert (data_out == model); // assertion passes (0 == 0)
en <= 1'b0; // en_driver
@(posedge clk);
This ordering now works because none of the DUT inputs are updated until the end of the time step, ensuring that all statements use the non-updated values. Let’s revisit the previous issue with the enable being updated:
@(posedge clk);
en <= 1'b0; // current = 1, future = 0
if (en) ... // monitor updates model because en is still 1
assert (data_out == model); // assertion passes because model is updated
etc.
Again, assigning the enable (with a non-blocking assignment) had no effect on the if statement because the enable’s value doesn’t change until the end of the time step. I’ll leave it as an exercise for you to explore different simulation orderings and see if they still work.
The epiphany I hope you’re having is that this type of race condition cannot occur when using non-blocking assignments. Although the simulator may execute the assignments at different times, their values are only applied at the end of the time step. Therefore, within a single time step, all processes will read the same value, regardless of the simulation order.
Conclusions and Final Thoughts
In this article, we’ve explored the most common causes of race conditions and presented a simple, general solution using non-blocking assignments. Although explaining the race conditions required a lengthy discussion, there are really just two key points to remember:
- Any signal assigned in one process and read in another—where both the assignment and the read are synchronized to the same event (e.g., a clock edge)—should be assigned using a non-blocking assignment.
- When writing a testbench, all assignments to DUT inputs should be made using non-blocking assignments.
Finally, don’t be tempted by “quick and dirty” solutions, such as adding wait statements in various places to try to resolve the race condition. Even if it seems to work, you might just be getting lucky with one particular simulation order. You should always identify the underlying cause of the race condition and implement a solution that works consistently across all simulation orders.
Similarly, don’t assume there’s a bug in the simulator just because it behaves differently from another simulator. While simulator bugs aren’t unheard of, this is more likely a sign of a race condition in your code. In fact, it’s a good idea to test your design in multiple simulators to help expose race conditions.
As a final piece of advice, I’ve encountered situations where someone is unwilling to make a change to their code to resolve a race condition because it “worked” before the change but doesn’t work afterward. The reality is that the code never truly worked. It only appeared to work because the simulator happened to choose an order that made it look like it did. If it doesn’t work after fixing a race condition, that’s actually a good thing—it means you’ve exposed a bug that needs to be fixed. While it’s human nature to resist changes to something that seems to work, it’s critically important as a hardware designer to understand that if a design only works in one simulation order, it doesn’t actually work.
Acknowledgements
I’d like to thank Chris Crary and Wes Piard for their valuable feedback.
