Retiming is a powerful optimization used in synthesis and digital-circuit design to improve the maximum clock frequency. Retiming works by relocating registers from paths with sufficient slack into paths with timing violations, essentially sacrificing slack from some paths to improve the timing of others—a strategy often referred to as “stealing slack.” For example:
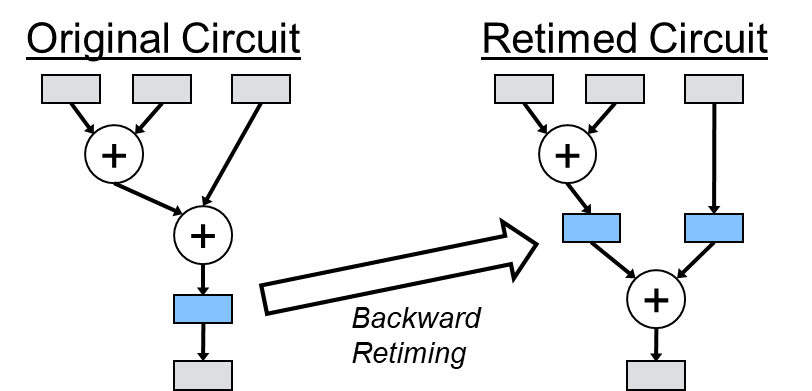
In this example, the timing of the path with two adders is improved by moving (i.e., retiming) the blue register into two registers between the adders. This optimization results in no path having a logic delay of more than a single adder. Although the delay of the second path is increased, the overall clock frequency is determined by the maximum delay across all paths. As a result, the retimed design can operate at approximately twice the clock speed, assuming negligible interconnect delays.
Throughout my decades of experience as a hardware designer, I’ve often heard engineers debate whether automatic retiming during synthesis can improve productivity by eliminating the need to worry about register placement in RTL code. For example, in a deep pipeline with 100 stages, a designer could theoretically simplify the RTL by placing all 100 registers at the beginning or end of the combinational logic, while relying on synthesis to move the registers to their optimal locations. In this article, we’ll evaluate retiming to determine whether it should be used solely as a synthesis optimization on an already well-designed circuit, or if it can serve as a productivity tool that allows designers to focus less on register locations. Alternatively, is there a middle ground where we can maximize productivity while still optimizing timing?
Retiming Overview
Background
Although the technical details of automatic retiming can be overwhelming, the basic concept is surprisingly simple: the goal of retiming is to reposition the registers in a digital circuit to maximize clock frequency. While some definitions of retiming allow for changes in a design’s latency, it is typically defined in a way that maintains identical latency (i.e., an n-stage pipeline must still take n cycles after retiming). Modifying latency is also a common optimization, often referred to as c-slowing, but it is generally considered a separate optimization from retiming. Additionally, c-slowing at the RTL level typically requires manual intervention, as RTL synthesis tools must preserve the latency specified in the RTL code. One advantage of high-level synthesis is its ability to automatically explore different latencies, since high-level code is untimed.
Retiming is often sub-classified by the direction in which a register moves. In backward retiming, registers are moved upstream, usually from the output of a combinational resource to the input, or possibly across multiple combinational resources. The two-adder example from the introduction is an example of backward retiming. Conversely, forward retiming moves registers from the inputs of a resource to the output of the same resource, or alternatively to a location further downstream in the circuit.
Note that retiming can significantly change the number of registers. Whenever a register is moved backward from the output of an operation, retiming must place a register on every input to that resource. For example, as shown earlier with an adder, backward retiming from the output would require two registers because the adder has two inputs. Similarly, forward retiming from the adder inputs to the output would reduce the number of registers from two to one. This reduction is a technique that can be applied manually to minimize the number of registers, as long as it doesn’t introduce timing violations.
Initial conditions, outputs, and c-cycle equivalence
Despite being conceptually simple, retiming involves a surprising number of complexities. As a result, engineers often get frustrated when synthesis tools don’t apply retiming in cases where it seems like an obvious optimization. However, there’s usually a good reason why retiming wasn’t applied.
One common reason retiming may fail is due to differing initial conditions and outputs. The following simple example illustrates this issue:
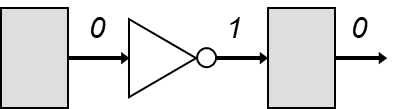
Assuming reset values of 0 for both flip-flops, the initial output of this example is 0. Now, let’s consider the backward retiming of this example:

Now, upon reset, the initial output is 1 because the register’s reset value of 0 is inverted. In other words, this circuit technically behaves differently from the original circuit. In such situations, retiming behavior may vary across synthesis tools, with some opting for a more conservative strategy that avoids retiming this example to ensure correctness. This conservative approach can be frustrating for designers, who may not care about the initial difference. However, synthesis tools often have no way of knowing the designer’s intent.
You may be wondering why this initial output difference matters, especially since it is often trivial to design a circuit that can ignore outputs for a given number of cycles. For example, pipelines commonly include control logic that disregards invalid outputs, such as those that may occur after a reset. If a circuit already ignores the initial output(s), retiming would be perfectly safe. The problem is that synthesis tools lack the ability to analyze the code and determine if specific outputs are ignored. As a result, retiming is often not applied, leading to frustration for designers.
To further highlight the problem, let’s extend the previous inverter example by attaching the inverter to a FIFO’s write enable signal:
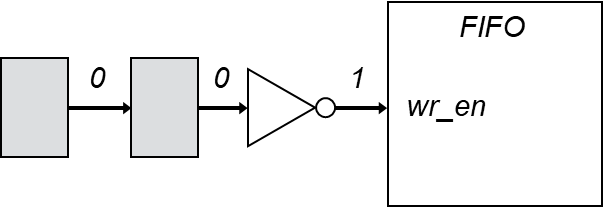
In this updated example, the initial behavior differences could cause unwanted data to be written into the FIFO on reset. In such a case, it is crucial for synthesis to avoid retiming the original example, as doing so would lead to the dreaded situation of discrepancies between simulated and synthesized behavior. While designers might be frustrated by retiming not being applied when they expect it, they would be furious if retiming were applied in a way that breaks the design. Given this risk, it’s not surprising that synthesis tools are conservative with retiming.
In some cases, synthesis tools allow for more aggressive retiming by letting the user specify that initial conditions can be ignored. While this strategy can be convenient, it is error-prone, as an incorrect assumption about the effect of differing initial conditions can lead to the generation of an incorrect design.
Alternatively, some retiming approaches use a concept called c-cycle equivalence, which analyzes initial conditions and determines that the behavior before and after retiming is equivalent after c cycles. Different synthesis tools handle c-cycle equivalence in various ways, with some even hiding it completely. For example, Intel/Altera Quartus retimes a design and provides a c-cycle equivalence report, allowing the user to know how long the reset sequence needs to be. I’ve come across papers discussing tools where the user can provide a c-cycle constraint to guide retiming, but I have not encountered a commercial tool that implements this approach.
In general, it’s important to consult the retiming documentation for your specific synthesis tool to understand any special considerations that must be addressed to ensure correctness.
Experiments
We’ll now examine a few specific examples to assess whether automatic retiming can enhance productivity. We will focus on CRC32, an adder tree, and multipliers of varying widths.
For all experiments, we use Vivado 2024.1 and target an UltraScale+ xcvu3p-ffvc1517-3-e. To enable retiming, we use -global_retiming on during synthesis, and -retime during physical optimization.
Example 1: CRC32
We’ll begin by examining CRC32, a widely used computation for error checking and hashing. Given its broad range of applications, CRC32 often has varying latency and throughput requirements, making it an ideal candidate for exploring productivity gains through automatic retiming. Instead of designing a pipeline tailored to a specific use case, we’ll describe the combinational logic and allow synthesis to retime a configurable number of registers.
The code below demonstrates a purely combinational implementation of IEEE 802.3 CRC32. While this code has been tested against other versions of IEEE 802.3 CRC32, it has not undergone the level of testing typically required for deployment. You are welcome to use it as open source at this time, but I do plan to perform more thorough testing and release an official version later, which will include additional features.
/*
Copyright (c) 2025 Gregory Stitt
Permission is hereby granted, free of charge, to any person obtaining a copy
of this software and associated documentation files (the "Software"), to deal
in the Software without restriction, including without limitation the rights
to use, copy, modify, merge, publish, distribute, sublicense, and/or sell
copies of the Software, and to permit persons to whom the Software is
furnished to do so, subject to the following conditions:
The above copyright notice and this permission notice shall be included in all
copies or substantial portions of the Software.
THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE
AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM,
OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE
SOFTWARE.
*/
module crc32_ieee_802_3 #(
parameter int DATA_WIDTH = 32
) (
input logic [DATA_WIDTH-1:0] data_in,
output logic [ 31:0] crc_out
);
logic [DATA_WIDTH-1:0] reflected_data;
logic [31:0] crc;
logic apply_polynomial;
initial if (DATA_WIDTH % 8 != 0) $fatal(1, "DATA_WIDTH must be byte aligned.");
always_comb begin
reflected_data = {<<8{{<<{data_in}}}};
crc = '1;
for (int i = DATA_WIDTH - 1; i >= 0; i--) begin
apply_polynomial = reflected_data[i] ^ crc[31];
crc = crc << 1;
if (apply_polynomial) crc = crc ^ 32'h04C11DB7;
end
crc_out = {<<{crc}} ^ 32'hFFFFFFFF;
end
endmoduleThis code is parameterized to support any data width to provide flexibility. However, as the data width increases, the maximum delay of the entity will also increase, eventually necessitating registers to meet timing requirements. While it’s common practice to break a large message into smaller blocks and apply CRC32 iteratively, we don’t want to impose this approach prematurely, as it could limit other use cases that prioritize lower latencies. Instead, we’ll maintain flexibility by using the purely combinational code and adding a configurable number of registers at either the input or output.
Note that when viewing the pre-synthesis schematic of this code, it may appear to contain an excessively long chain of logic operations. However, during synthesis, this chain is optimized and reduced to just a few levels of logic.
First, we’ll evaluate forward retiming using the following code:
// Greg Stitt
// StittHub (stitt-hub.com)
module crc32_forward #(
parameter int DATA_WIDTH = 128,
parameter int LATENCY = 2
) (
input logic clk,
input logic [DATA_WIDTH-1:0] data_in,
output logic [ 31:0] crc_out
);
(* srl_style = "register" *) logic [DATA_WIDTH-1:0] data_in_r[LATENCY];
always_ff @(posedge clk) begin
data_in_r[0] <= data_in;
for (int i = 1; i < LATENCY; i++) data_in_r[i] <= data_in_r[i-1];
end
crc32_ieee_802_3 #(
.DATA_WIDTH(DATA_WIDTH)
) crc32 (
.data_in(data_in_r[LATENCY-1]),
.crc_out(crc_out)
);
endmoduleThis code simply adds LATENCY registers before the CRC32, with the hope that synthesis will retime them into the CRC’s combinational logic. One important detail to note is the srl_style attribute. I added this because, in my initial experiments, Vivado packed all the registers into SRL primitives. It wasn’t clear that SRL registers were being retimed, so I included the attribute to force Vivado to use regular registers instead. While I didn’t evaluate this code in Quartus, I have encountered similar situations where a long chain of registers gets implemented in block RAM, which is also unlikely to be retimed. Keep an eye out for such technology mappings. If you notice the synthesis tool using resources you don’t want, there is usually a set of attributes that can force the tool to use other resources.
The potential drawback of forward retiming in this example is that if synthesis doesn’t find the optimal solution (or apply it at all), adding registers at the beginning of the pipeline could unnecessarily increase the number of registers. For any reduction circuit, there are typically more inputs than outputs, so adding extra registers to the inputs will require more resources than adding them to the outputs.
Next, we’ll explore the opposite approach by applying backward retiming, placing extra registers at the output of the design:
// Greg Stitt
// StittHub (stitt-hub.com)
module crc32_backward #(
parameter int DATA_WIDTH = 128,
parameter int LATENCY = 2
) (
input logic clk,
input logic [DATA_WIDTH-1:0] data_in,
output logic [ 31:0] crc_out
);
(* srl_style = "register" *) logic [31:0] crc_r[LATENCY];
logic [31:0] crc;
crc32_ieee_802_3 #(
.DATA_WIDTH(DATA_WIDTH)
) crc32 (
.data_in(data_in),
.crc_out(crc)
);
always_ff @(posedge clk) begin
crc_r[0] <= crc;
for (int i = 1; i < LATENCY; i++) crc_r[i] <= crc_r[i-1];
end
assign crc_out = crc_r[LATENCY-1];
endmoduleThe figure below illustrates the clock frequencies achieved through forward retiming across three different message sizes, with two pipelining depths:
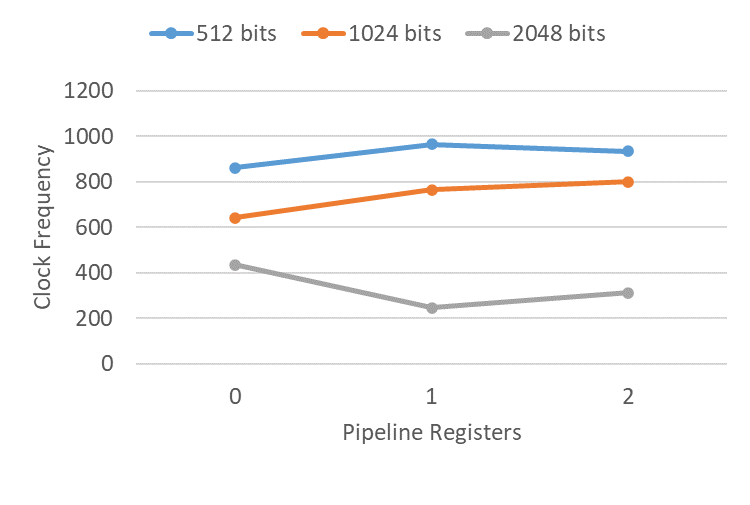
1024-bit messages showed modest clock improvements from retiming with both one and two additional registers. 512-bit messages showed an improved frequency with one additional register, but a decrease in frequency with two registers. The 2048-bit message, however, showed a considerable decrease in performance when retimed. Upon further investigation, CRC32 on a 2048-bit message caused significant congestion, which was apparently worsened by the retimed registers. While none of these cases achieved the level of improvement typically expected from pipelining, a few experienced clock improvements that could be considered significant for certain use cases.
The following figure presents similar experiments for backward retiming of CRC32, which showed trends comparable to those of forward retiming:
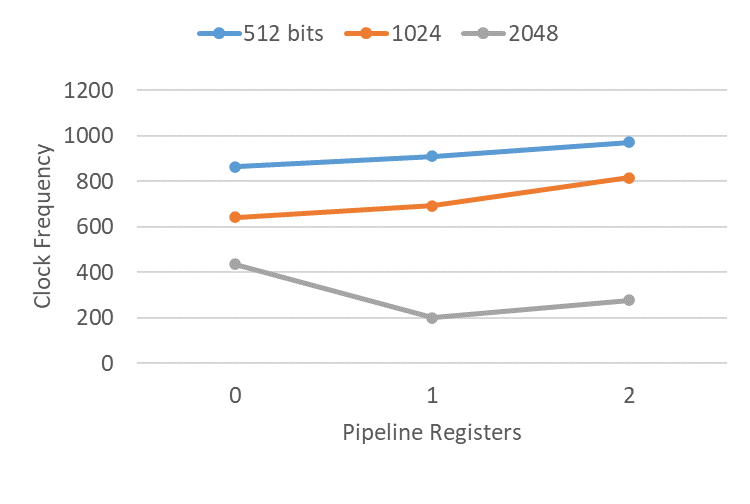
Overall, these results suggest that if you’re working with message sizes of 1024 bits or smaller, retiming can be a useful productivity booster, as the RTL code doesn’t explicitly need to account for register locations or subdivide the message into smaller chunks. However, to support arbitrary message sizes, the circuit will generally need to be designed to process the message iteratively. While I haven’t created that circuit myself yet, I would expect it to yield significant improvements in clock frequency and resource utilization. The code we used here is likely more suitable for low-latency hashing scenarios where an increase in resources is acceptable.
An interesting follow-up study would be to evaluate these same experiments on older FPGA families. In my experience, UltraScale+ achieves significantly higher clock frequencies than earlier FPGA generations. If you’re still working with an older FPGA, it’s possible that retiming could result in substantial percentage improvements.
Example 2: Adder Tree
In the previous example, we began with pure combinational logic and used retiming to move registers into the middle of that logic. In this example, we’ll start with an optimized pipeline and explore how closely we can replicate that pipeline using combinational logic and retiming.
For this example, we’ll use the recursive adder tree pipeline from my earlier StittHub article, You Can (and Should) Write Recursive RTL: Part 2. This code serves as an excellent baseline, as it has been manually optimized and can support any number of inputs. To test it with retiming, we’ll simply remove the registers from the adder tree, as shown below:
// Greg Stitt
// StittHub (stitt-hub.com)
module add_tree_comb #(
parameter int NUM_INPUTS = 8,
parameter int INPUT_WIDTH = 16
) (
input logic [ INPUT_WIDTH-1:0] inputs[NUM_INPUTS],
output logic [INPUT_WIDTH+$clog2(NUM_INPUTS)-1:0] sum
);
generate
if (INPUT_WIDTH < 1) begin : l_width_validation
$fatal(1, "ERROR: INPUT_WIDTH must be positive.");
end
if (NUM_INPUTS < 1) begin : l_num_inputs_validation
$fatal(1, "ERROR: Number of inputs must be positive.");
end else if (NUM_INPUTS == 1) begin : l_base_1_input
assign sum = inputs[0];
end else begin : l_recurse
//--------------------------------------------------------------------
// Create the left subtree
//--------------------------------------------------------------------
localparam int LEFT_TREE_INPUTS = int'(2 ** ($clog2(NUM_INPUTS) - 1));
localparam int LEFT_TREE_DEPTH = $clog2(LEFT_TREE_INPUTS);
logic [INPUT_WIDTH + $clog2(LEFT_TREE_INPUTS)-1:0] left_sum;
add_tree_comb #(
.NUM_INPUTS (LEFT_TREE_INPUTS),
.INPUT_WIDTH(INPUT_WIDTH)
) left_tree (
.inputs(inputs[0+:LEFT_TREE_INPUTS]),
.sum (left_sum)
);
//--------------------------------------------------------------------
// Create the right subtree.
//--------------------------------------------------------------------
localparam int RIGHT_TREE_INPUTS = NUM_INPUTS - LEFT_TREE_INPUTS;
localparam int RIGHT_TREE_DEPTH = $clog2(RIGHT_TREE_INPUTS);
logic [INPUT_WIDTH + $clog2(RIGHT_TREE_INPUTS)-1:0] right_sum, right_sum_unaligned;
add_tree_comb #(
.NUM_INPUTS (RIGHT_TREE_INPUTS),
.INPUT_WIDTH(INPUT_WIDTH)
) right_tree (
.inputs(inputs[LEFT_TREE_INPUTS+:RIGHT_TREE_INPUTS]),
.sum (right_sum)
);
// Add the two trees together.
assign sum = left_sum + right_sum;
end
endgenerate
endmoduleNext, we’ll write the code to apply forward and backward retiming to this combinational adder tree:
// Greg Stitt
// StittHub (stitt-hub.com)
module add_tree_forward #(
parameter int NUM_INPUTS = 8,
parameter int INPUT_WIDTH = 16,
parameter int LATENCY = 2
) (
input logic clk,
input logic rst,
input logic en,
input logic [ INPUT_WIDTH-1:0] inputs[NUM_INPUTS],
output logic [INPUT_WIDTH+$clog2(NUM_INPUTS)-1:0] sum
);
typedef logic [INPUT_WIDTH-1:0] input_array[NUM_INPUTS];
(* srl_style = "register" *) input_array inputs_r[LATENCY];
always_ff @(posedge clk) begin
if (en) begin
inputs_r[0] <= inputs;
for (int i = 1; i < LATENCY; i++) inputs_r[i] <= inputs_r[i-1];
end
if (rst) inputs_r <= '{default: '{default: '0}};
end
add_tree_comb #(
.NUM_INPUTS (NUM_INPUTS),
.INPUT_WIDTH(INPUT_WIDTH)
) DUT (
.inputs(inputs_r[LATENCY-1]),
.sum (sum)
);
endmodule// Greg Stitt
// StittHub (stitt-hub.com)
module add_tree_backward #(
parameter int NUM_INPUTS = 8,
parameter int INPUT_WIDTH = 16,
parameter int LATENCY = 2
) (
input logic clk,
input logic rst,
input logic en,
input logic [ INPUT_WIDTH-1:0] inputs[NUM_INPUTS],
output logic [INPUT_WIDTH+$clog2(NUM_INPUTS)-1:0] sum
);
(* srl_style = "register" *) logic [INPUT_WIDTH+$clog2(NUM_INPUTS)-1:0] sum_r[LATENCY];
logic [INPUT_WIDTH+$clog2(NUM_INPUTS)-1:0] sum_in;
add_tree_comb #(
.NUM_INPUTS (NUM_INPUTS),
.INPUT_WIDTH(INPUT_WIDTH)
) DUT (
.inputs(inputs),
.sum (sum_in)
);
always_ff @(posedge clk) begin
if (en) begin
sum_r[0] <= sum_in;
for (int i = 1; i < LATENCY; i++) sum_r[i] <= sum_r[i-1];
end
if (rst) sum_r <= '{default: '0};
end
assign sum = sum_r[LATENCY-1];
endmoduleFor this example, I preserved the reset and enable from the original adder tree to ensure a fair comparison. While this might suggest that the srl_style attribute is now unnecessary (since registers with a reset can’t be mapped into SRLs), I kept the attribute in place because my top-level entity (not shown) hardcodes the reset to 0 and the enable to 1 to maximize clock frequency for all tests.
The code below shows the clock frequencies resulting from forward retiming of adder trees with 32 to 256 inputs, where each input is 16 bits. The rightmost point (manual) represents the frequency of the original, manually pipelined code.
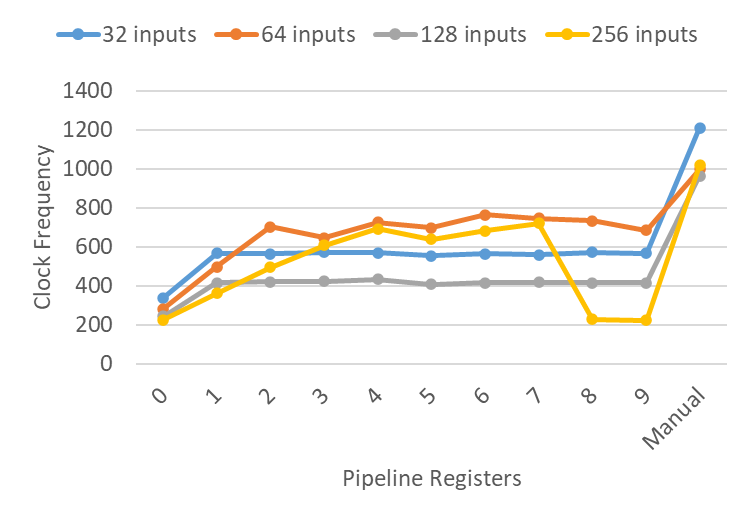
While retiming shows some initial improvement as registers are added, the clock frequencies quickly plateau, with no further gains. There are also occasional, unexpected drops in performance. For instance, the 256-input adder tree with 8-9 registers achieved the same performance as the pure combinational logic.
Overall, the percentage improvements of the manual pipelines compared to the maximum clock frequencies of the retimed examples were 111%, 30%, 122%, and 41%, respectively, across the different input sizes. Given these significant improvements and the lack of a clear productivity advantage from retiming, manual pipelining emerges as the clear winner in this case.
One result I found particularly interesting was how well the purely combinational logic adder tree performed for 128 and 256 inputs. I wouldn’t have expected a 256-input adder tree to achieve a clock frequency anywhere near 226 MHz. Upon further investigation, the result isn’t as surprising but is still quite intriguing. Each time the adder tree doubles in size, the depth of the tree increases by just a single adder. Ignoring interconnect delays, this suggests that the delay should increase logarithmically with the number of inputs, which is exactly what we’re seeing in these results. However, in my experience, these types of results can change dramatically when the circuit is integrated into a larger design, where routing congestion and placement constraints prevent achieving this ideal logarithmic delay complexity. In any case, these results highlight the need for a future StittHub article exploring different adder architectures.
The following chart shows the same experiments for backward retiming:
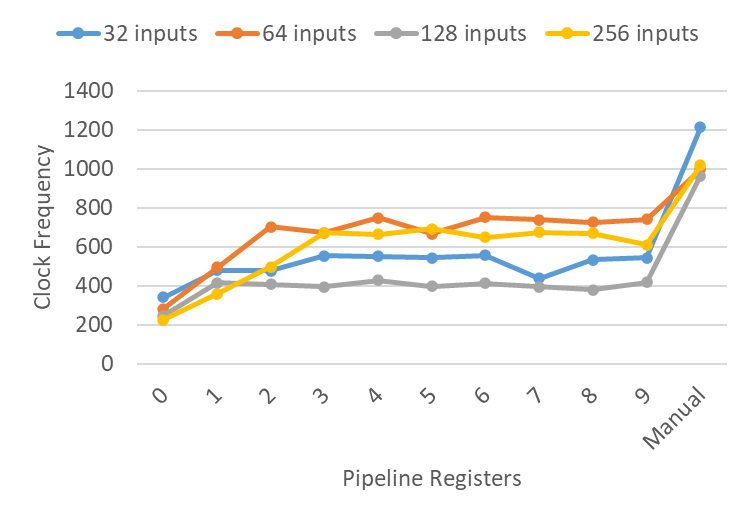
Overall, these results show similar trends, with retiming failing to match the clock frequencies achieved by manual pipelining. Manual pipelining was 117%, 32%, 126%, and 47% faster across the different input sizes, respectively. Backward retiming avoided the previous drop for 8-9 registers at 256 inputs, which suggests backward retiming might be more effective than forward. However, I don’t believe there is enough data to conclude that with any certainty. Placement and routing is known for having weird outliers such as this.
Example 3: Multiplier
In this third example, we’ll explore a conceptually similar case, where we attempt to pipeline wide multiplications automatically through retiming. DSP resources used for multiplication generally have optional internal registers that can be explicitly utilized. However, manually enabling those registers in RTL code can sometimes be cumbersome, especially when writing code intended to be portable across different FPGAs. It would be convenient if we could write RTL using a multiplication operator, followed by a configurable number of registers.
For the baseline code, we’ll simply use a standard multiplier:
// Greg Stitt
// StittHub (stitt-hub.com)
module mult #(
parameter int INPUT_WIDTH = 16
) (
input logic [ INPUT_WIDTH-1:0] in0,
input logic [ INPUT_WIDTH-1:0] in1,
output logic [2*INPUT_WIDTH-1:0] product
);
assign product = in0 * in1;
endmoduleAs before, we’ll evaluate both forward and backward retiming. The forward retiming code is shown below:
// Greg Stitt
// StittHub (stitt-hub.com)
module mult_forward #(
parameter int INPUT_WIDTH = 16,
parameter int LATENCY = 2
) (
input logic clk,
input logic rst,
input logic en,
input logic [ INPUT_WIDTH-1:0] in0,
input logic [ INPUT_WIDTH-1:0] in1,
output logic [2*INPUT_WIDTH-1:0] product
);
(* srl_style = "register" *) logic [2*INPUT_WIDTH-1:0] inputs_r[LATENCY];
logic [INPUT_WIDTH-1:0] in0_r, in1_r;
always_ff @(posedge clk) begin
if (en) begin
inputs_r[0] <= {in0, in1};
for (int i = 1; i < LATENCY; i++) inputs_r[i] <= inputs_r[i-1];
end
if (rst) inputs_r <= '{default: '0};
end
assign {in0_r, in1_r} = inputs_r[LATENCY-1];
assign product = in0_r * in1_r;
endmoduleThe backward retiming code is similar:
// Greg Stitt
// StittHub (stitt-hub.com)
module mult_backward #(
parameter int INPUT_WIDTH = 16,
parameter int LATENCY = 2
) (
input logic clk,
input logic rst,
input logic en,
input logic [ INPUT_WIDTH-1:0] in0,
input logic [ INPUT_WIDTH-1:0] in1,
output logic [2*INPUT_WIDTH-1:0] product
);
(* srl_style = "register" *) logic [2*INPUT_WIDTH-1:0] product_r[LATENCY];
always_ff @(posedge clk) begin
if (en) begin
product_r[0] <= in0 * in1;
for (int i = 1; i < LATENCY; i++) product_r[i] <= product_r[i-1];
end
if (rst) product_r <= '{default: '0};
end
assign product = product_r[LATENCY-1];
endmoduleThe following figure displays the clock frequencies achieved through forward retiming for four different multiplier widths:
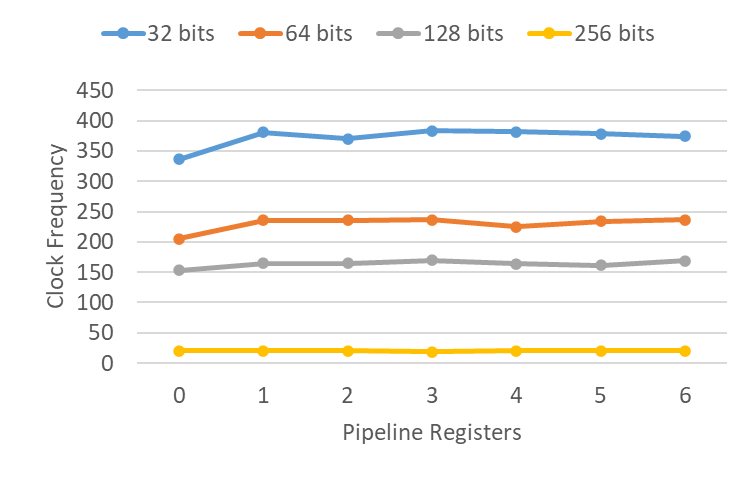
Interestingly, forward retiming essentially achieved no improvement, with the slight differences primarily being placement and routing noise. There is a simple explanation for this, but first, let’s examine the backward retiming results:
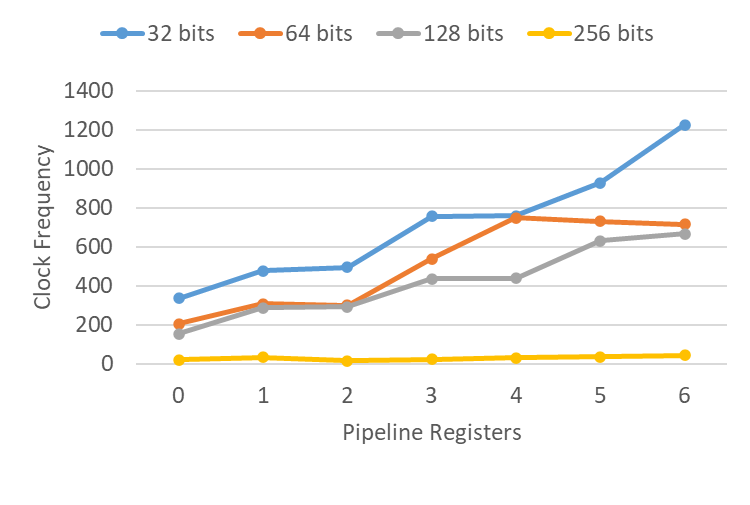
For all multiplier widths except the 256-bit case, we generally observe significant improvements in clock frequency as more registers are added. The 256-bit multiplier showed no improvement, but I included this example mainly as a stress test. I’ve never encountered a 256-bit multiplier in practice, so it’s likely that Vivado lacks built-in optimizations for such a large size.
So, why did backward retiming work well here when forward retiming failed? The key difference is that it’s not just retiming at play here. This example is more about an optimization known as packing. Packing involves coalescing finer-grained operations into a coarser-grained resource. In this case, the coarse-grained resource is a DSP unit, which, in addition to the multiplier, includes other resources such as registers. When Vivado (and most synthesis tools) pack registers into DSPs, they typically look for registers on the output of the DSP. While it’s theoretically possible for forward retiming to move the registers to the DSP’s output to enable packing, it is unlikely that any synthesis tool would consider doing this on its own.
Although I don’t have a manually pipelined multiplier for comparison, I consider this backward retiming with packing strategy to be highly effective. In fact, the reason I don’t have a manually pipelined multiplier is that this packing strategy has almost always met timing requirements for my applications. When it hasn’t, I’ve simply used multiplier IP from each FPGA vendor. While I’m sure there are some compelling trade-offs to manually pipelined multipliers, I’ve never needed them. Therefore, I would strongly recommend using code similar to this example, where you select a number of registers that meets your clock constraint.
Conclusions
In this article, we explored the potential of using retiming as a productivity booster. Instead of manually pipelining designs, we described the design using combinational logic with registers at the beginning or end, then relied on retiming to move those registers to their optimal locations
The three experiments demonstrated that retiming cannot be relied on to yield the ideal pipeline. For the adder-tree example, manual pipelining sometimes achieved clock frequencies that were twice as fast as those achieved by retiming.
While retiming doesn’t provide the perfect pipelining solution, the experiments did show that it can offer a “good-enough” solution in certain cases. If manually pipelining a design is time-consuming, while describing the combinational logic is trivial, it may be worth testing whether retiming can meet timing constraints.
In conclusion, retiming can be a productivity tool in specific scenarios, but it is not a substitute for manual pipelining.
Acknowledgements
I’d like to thank Wes Piard for his feedback on the CRC32 code, and Chris Crary and Jackson Fugate for their input on the article. I’d also like to acknowledge the University of Florida for providing access to their servers and tool licenses.
